[This article was migrated to the author’s GitHub Pages site here in July 2025]
In my last post, A Design Pattern for Oracle eBusiness Audit Trail Reports with XML Publisher, I described a database report module developed in Oracle’s XML Publisher tool. Of the report structure I wrote:
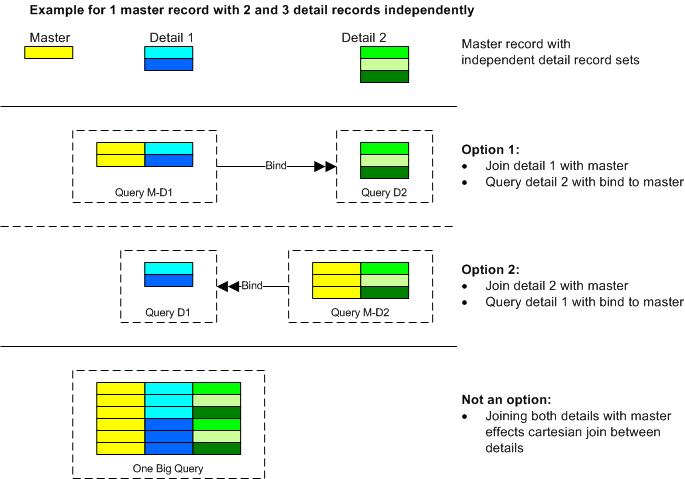
It has a master entity with two independent detail entities, and therefore requires a minimum of two queries.
But why does such a structure require two queries? And can we determine the minimum number of queries for reports in general? To start with, let’s define a report in this context as being a hierarchy of record groups, where:
- a record group is a set of records having the same columns with (possibly) differing values
- each group is linked to a single record in its (single) parent group by values in the parent record, except the top level (or root) group
For example, in the earlier post the root group is a set of bank accounts, with the two detail (or child) groups being the set of owners of the bank account and the set of audit records for the bank account parent record. Corresponding to this group structure, each bank account record is the root of the data hierarchies, comprising two sets of records below the bank account record, one for the owners and one for the audit records linked to the root record by the bank account id.
A (relational) query always returns a flat record set, and it’s this fact that determines the minimum number of queries required for a given group structure. A master-detail group structure can be flattened in the query by simply copying master fields on to the child record sets. The set cardinality is then the cardinality of the child set. The report designer uses their chosen reporting tool to specify display of the queried data in either flat, or in master-detail format.
In fact this approach works for any number of child levels, with the query cardinality being the number of bottom level descendants (using null records for potential parents that are in fact childless). It’s clear though that the approach will not work for any second child at the same level because there would be two cardinalities and no meaningful single record for both child groups could be constructed within a flat query.
This reasoning leads to the conclusion that the minimum number of queries required in general is equal to the number of groups minus the number of parent groups.
In the earlier post I also stated:
This minimum number of queries is usually the best choice…
There are two main reasons for this:
- each child query fires for every record returned by its parent, with associated performance impact
- maintenance tends to be more difficult with extra queries; this is much worse when the individual groups, which should almost always be implemented by a maximum of one query each, are split, and then need to be joined back together procedurally
On thinking about this, it occurred to me that if the group structure were defined in a metadata table we might be able to return minimum query structures using an SQL query. Just one, obviously 🙂 . To save effort we could use Oracle’s handy HR demo schema with the employee hierarchy representing groups.
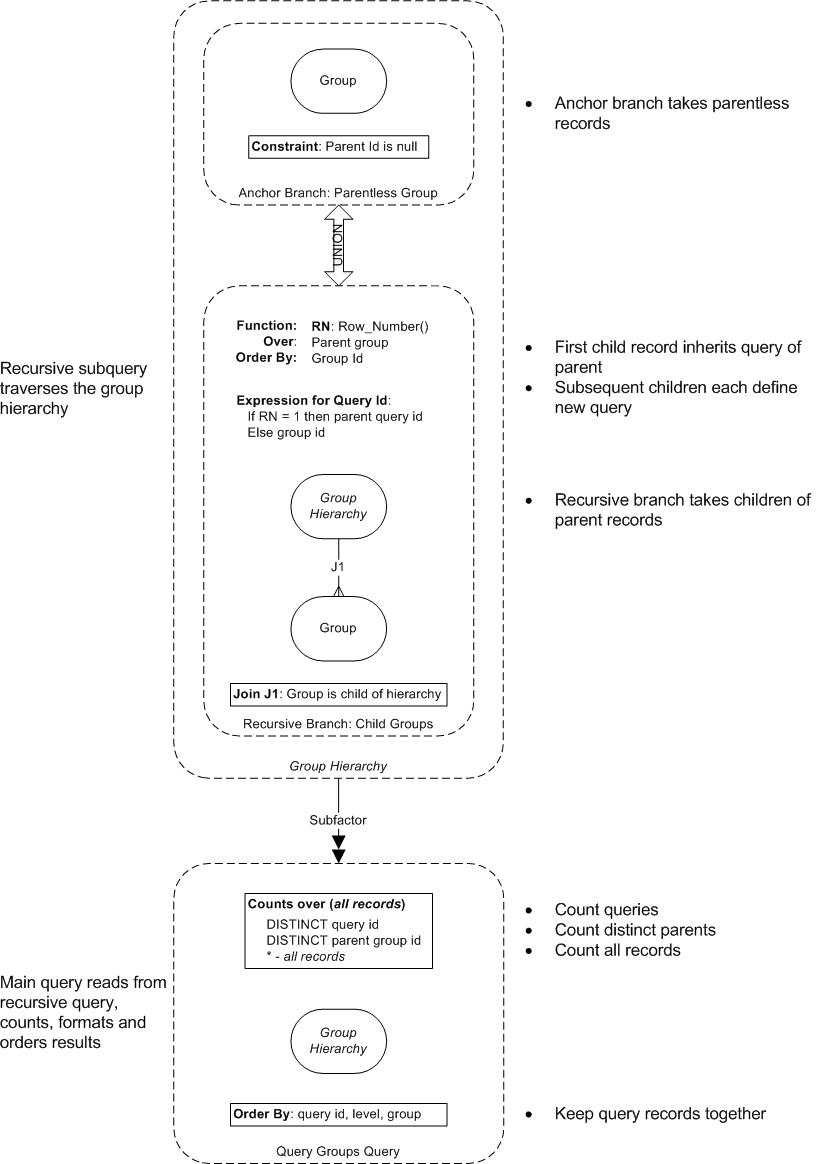
The remainder of this article describes the query I came up with. As it’s about hierarchies, recursion is the technique to use, and this is one of those cases where Oracle’s old tree-walk syntax is too limited, so I am using the Oracle 11.2 recursive subquery factoring feature.
The query isn’t going to be of practical value for report group structures since these are always quite small in size, but I expect there are different applications where this kind of Primogeniture Recursion would be useful.
Query Groups Query – Primogeniture Recursion
SQL
WITH rsf (last_name, employee_id, lev, part_id, manager_id) AS (
SELECT last_name, employee_id, 0, employee_id, To_Number(NULL)
FROM employees
WHERE manager_id IS NULL
UNION ALL
SELECT e.last_name, e.employee_id, r.lev + 1,
CASE WHEN Row_Number() OVER (PARTITION BY r.employee_id ORDER BY e.last_name) = 1 THEN r.part_id ELSE e.employee_id END,
e.manager_id
FROM rsf r
JOIN employees e
ON e.manager_id = r.employee_id
)
SELECT part_id, LPad ('.', lev) || last_name last_name, employee_id,
Count(DISTINCT part_id) OVER () "#Partitions",
Count(DISTINCT manager_id) OVER () "+ #Parents",
Count(*) OVER () "= #Records"
FROM rsf
ORDER BY part_id, lev, last_name
Query Output
PART_ID LAST_NAME EMPLOYEE_ID #Partitions + #Parents = #Records
---------- -------------------- ----------- ----------- ---------- ----------
100 King 100 89 18 107
.Cambrault 148 89 18 107
.Bates 172 89 18 107
101 .Kochhar 101 89 18 107
.Baer 204 89 18 107
102 .De Haan 102 89 18 107
.Hunold 103 89 18 107
.Austin 105 89 18 107
104 .Ernst 104 89 18 107
106 .Pataballa 106 89 18 107
107 .Lorentz 107 89 18 107
108 .Greenberg 108 89 18 107
.Chen 110 89 18 107
109 .Faviet 109 89 18 107
111 .Sciarra 111 89 18 107
112 .Urman 112 89 18 107
113 .Popp 113 89 18 107
114 .Raphaely 114 89 18 107
.Baida 116 89 18 107
115 .Khoo 115 89 18 107
117 .Tobias 117 89 18 107
118 .Himuro 118 89 18 107
119 .Colmenares 119 89 18 107
120 .Weiss 120 89 18 107
.Fleaur 181 89 18 107
121 .Fripp 121 89 18 107
.Atkinson 130 89 18 107
122 .Kaufling 122 89 18 107
.Chung 188 89 18 107
123 .Vollman 123 89 18 107
.Bell 192 89 18 107
124 .Mourgos 124 89 18 107
.Davies 142 89 18 107
125 .Nayer 125 89 18 107
126 .Mikkilineni 126 89 18 107
127 .Landry 127 89 18 107
128 .Markle 128 89 18 107
129 .Bissot 129 89 18 107
131 .Marlow 131 89 18 107
132 .Olson 132 89 18 107
133 .Mallin 133 89 18 107
134 .Rogers 134 89 18 107
135 .Gee 135 89 18 107
136 .Philtanker 136 89 18 107
137 .Ladwig 137 89 18 107
138 .Stiles 138 89 18 107
139 .Seo 139 89 18 107
140 .Patel 140 89 18 107
141 .Rajs 141 89 18 107
143 .Matos 143 89 18 107
144 .Vargas 144 89 18 107
145 .Russell 145 89 18 107
.Bernstein 151 89 18 107
146 .Partners 146 89 18 107
.Doran 160 89 18 107
147 .Errazuriz 147 89 18 107
.Ande 166 89 18 107
149 .Zlotkey 149 89 18 107
.Abel 174 89 18 107
150 .Tucker 150 89 18 107
152 .Hall 152 89 18 107
153 .Olsen 153 89 18 107
154 .Cambrault 154 89 18 107
155 .Tuvault 155 89 18 107
156 .King 156 89 18 107
157 .Sully 157 89 18 107
158 .McEwen 158 89 18 107
159 .Smith 159 89 18 107
161 .Sewall 161 89 18 107
162 .Vishney 162 89 18 107
163 .Greene 163 89 18 107
164 .Marvins 164 89 18 107
165 .Lee 165 89 18 107
167 .Banda 167 89 18 107
168 .Ozer 168 89 18 107
169 .Bloom 169 89 18 107
170 .Fox 170 89 18 107
171 .Smith 171 89 18 107
173 .Kumar 173 89 18 107
175 .Hutton 175 89 18 107
176 .Taylor 176 89 18 107
177 .Livingston 177 89 18 107
178 .Grant 178 89 18 107
179 .Johnson 179 89 18 107
180 .Taylor 180 89 18 107
182 .Sullivan 182 89 18 107
183 .Geoni 183 89 18 107
184 .Sarchand 184 89 18 107
185 .Bull 185 89 18 107
186 .Dellinger 186 89 18 107
187 .Cabrio 187 89 18 107
189 .Dilly 189 89 18 107
190 .Gates 190 89 18 107
191 .Perkins 191 89 18 107
193 .Everett 193 89 18 107
194 .McCain 194 89 18 107
195 .Jones 195 89 18 107
196 .Walsh 196 89 18 107
197 .Feeney 197 89 18 107
198 .OConnell 198 89 18 107
199 .Grant 199 89 18 107
200 .Whalen 200 89 18 107
201 .Hartstein 201 89 18 107
.Fay 202 89 18 107
203 .Mavris 203 89 18 107
205 .Higgins 205 89 18 107
.Gietz 206 89 18 107
107 rows selected.

Oracle mentions an interesting alternative, called the “union join”, in the context of JSON support: http://docs.oracle.com/database/121/ADXDB/json.htm#ADXDB6287
Function JSON_TABLE allows for multiple NESTED COLUMNS clauses, including siblings. “The virtual tables defined by parent and child COLUMNS clauses are joined using an outer join, with the parent being the outer table. The virtual columns defined by sibling COLUMNS clauses are joined using a union join.”
The UNION JOIN is equivalent to a FULL JOIN…ON 1=0;
The same technique could be used for any “family tree” of real tables.