[This article was migrated to the author’s GitHub Pages site here in July 2025]
I noticed a post on AskTom recently that referred to an SQL solution to a version of the so-called Bin Fitting problem, where even distribution is the aim. The solution, [How do I solve a Bin Fitting problem in an SQL statement? (link no longer available on 19 July 2025)], uses Oracle’s Model clause, and, as the poster of the link observed, has the drawback that the number of bins is embedded in the query structure. I thought it might be interesting to find solutions without that drawback, so that the number of bins could be passed to the query as a bind variable. I came up with three solutions using different techniques, starting here.
An interesting article in American Scientist, The Easiest Hard Problem, notes that the problem is NP-complete, or certifiably hard, but that simple greedy heuristics often produce a good solution, including one used by schoolboys to pick football teams. The article uses the more descriptive term for the problem of balanced number partitioning, and notes some practical applications. The Model clause solution implements a multiple-bin version of the main Greedy Algorithm, while my non-Model SQL solutions implement variants of it that allow other techniques to be used, one of which is very simple and fast: this implements the team picking heuristic for multiple teams.
Another poster, Stew Ashton, suggested a simple change to my Model solution that improved performance, and I use this modified version here. He also suggested that using PL/SQL might be faster, and I have added my own simple PL/SQL implementation of the Greedy Algorithm, as well as a second version of the recursive subquery factoring solution that performs better than the first.
This article explains the solutions, considers two simple examples to illustrate them, and reports on performance testing across dimensions of number of items and number of bins. These show that the solutions exhibit either linear or quadratic variation in execution time with number of items, and some methods are sensitive to the number of bins while others are not.
After I had posted my solutions on the AskTom thread, I came across a thread on OTN, need help to resolve this issue, that requested a solution to a form of bin fitting problem where the bins have fixed capacity and the number of bins required must be determined. I realised that my solutions could easily be extended to add that feature, and posted extended versions of two of the solutions there. I have added a section here for this.
Updated, 5 June 2013: added Model and RSF diagrams
Update, 18 November 2017: I have now put scripts for setting up data and running the queries in a new schema onto my GitHub project: Brendan’s repo for interesting SQL. Note that I have not included the minor changes needed for the extended problem where finding the number of bins is part of the problem.
Greedy Algorithm Variants
Say there are N bins and M items.
Greedy Algorithm (GDY)
Set bin sizes zero
Loop over items in descending order of size
- Add item to current smallest bin
- Calculate new bin size
End Loop
Greedy Algorithm with Batched Rebalancing (GBR)
Set bin sizes zero
Loop over items in descending order of size in batches of N items
- Assign batch to N bins, with bins in ascending order of size
- Calculate new bin sizes
End Loop
Greedy Algorithm with No Rebalancing – or, Team Picking Algorithm (TPA)
Assign items to bins cyclically by bin sequence in descending order of item size
Two Examples
Example: Four Items

Here we see that the Greedy Algorithm finds the perfect solution, with no difference in bin size, but the two variants have a difference of two.
Example: Six Items
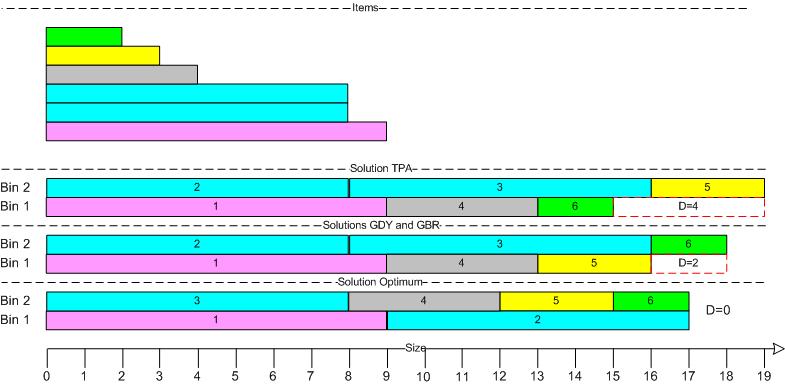
Here we see that none of the algorithms finds the perfect solution. Both the standard Greedy Algorithm and its batched variant give a difference of two, while the variant without rebalancing gives a difference of four.
SQL Solutions
Original Model for GDY
See the link above for the SQL for the problem with three bins only.
The author has two measures for each bin and implements the GDY algorithm using CASE expressions and aggregation within the rules. The idea is to iterate over the items in descending order of size, setting the item bin to the bin with current smallest value. I use the word ‘bin’ for his ‘bucket’. Some notes:
- Dimension by row number, ordered by item value
- Add measures for the iteration, it, and number of iterations required, counter
- Add measures for the bin name, bucket_name, and current minimum bin value, min_tmp (only first entry used)
- Add measures for each item bin value, bucket_1-3, being the item value if it’s in that bin, else zero
- Add measures for each bin running sum, pbucket_1-3, being the current value of each bin (only first two entries used)
- The current minimum bin value, bin_tmp[1] is computed as the least of the running sums
- The current item bin value is set to the item value for the bin whose value matches the minimum just computed, and null for the others
- The current bin name is set similarly to be the bin matching the minimum
- The new running sums are computed for each bin
Brendan’s Generic Model for GDY
SELECT item_name, bin, item_value, Max (bin_value) OVER (PARTITION BY bin) bin_value
FROM (
SELECT * FROM items
MODEL
DIMENSION BY (Row_Number() OVER (ORDER BY item_value DESC) rn)
MEASURES (item_name,
item_value,
Row_Number() OVER (ORDER BY item_value DESC) bin,
item_value bin_value,
Row_Number() OVER (ORDER BY item_value DESC) rn_m,
0 min_bin,
Count(*) OVER () - :N_BINS - 1 n_iters
)
RULES ITERATE(100000) UNTIL (ITERATION_NUMBER >= n_iters[1]) (
min_bin[1] = Min(rn_m) KEEP (DENSE_RANK FIRST ORDER BY bin_value)[rn <= :N_BINS],
bin[ITERATION_NUMBER + :N_BINS + 1] = min_bin[1],
bin_value[min_bin[1]] = bin_value[CV()] + Nvl (item_value[ITERATION_NUMBER + :N_BINS + 1], 0)
)
)
WHERE item_name IS NOT NULL
ORDER BY item_value DESC
My Model solution works for any number of bins, passing the number of bins as a bind variable. The key idea here is to use values in the first N rows of a generic bin value measure to store all the running bin values, rather than as individual measures. I have included two modifications suggested by Stew in the AskTom thread.
- Dimension by row number, ordered by item value
- Initialise a bin measure to the row number (the first N items will remain fixed)
- Initialise a bin value measure to item value (only first N entries used)
- Add the row number as a measure, rn_m, in addition to a dimension, for referencing purposes
- Add a min_bin measure for current minimum bin index (first entry only)
- Add a measure for the number of iterations required, n_iters
- The first N items are correctly binned in the measure initialisation
- Set the minimum bin index using analytic Min function with KEEP clause over the first N rows of bin value
- Set the bin for the current item to this index
- Update the bin value for the corresponding bin only

Recursive Subquery Factor for GBR
WITH bins AS (
SELECT LEVEL bin, :N_BINS n_bins FROM DUAL CONNECT BY LEVEL <= :N_BINS
), items_desc AS (
SELECT item_name, item_value, Row_Number () OVER (ORDER BY item_value DESC) rn
FROM items
), rsf (bin, item_name, item_value, bin_value, lev, bin_rank, n_bins) AS (
SELECT b.bin,
i.item_name,
i.item_value,
i.item_value,
1,
b.n_bins - i.rn + 1,
b.n_bins
FROM bins b
JOIN items_desc i
ON i.rn = b.bin
UNION ALL
SELECT r.bin,
i.item_name,
i.item_value,
r.bin_value + i.item_value,
r.lev + 1,
Row_Number () OVER (ORDER BY r.bin_value + i.item_value),
r.n_bins
FROM rsf r
JOIN items_desc i
ON i.rn = r.bin_rank + r.lev * r.n_bins
)
SELECT r.item_name,
r.bin, r.item_value, r.bin_value
FROM rsf r
ORDER BY item_value DESC
The idea here is to use recursive subquery factors to iterate through the items in batches of N items, assigning each item to a bin according to the rank of the bin on the previous iteration.
- Initial subquery factors form record sets for the bins and for the items with their ranks in descending order of value
- The anchor branch assign bins to the first N items, assigning the item values to a bin value field, and setting the bin rank in ascending order of this bin value
- The recursive branch joins the batch of items to the record in the previous batch whose bin rank matches that of the item in the reverse sense (so largest item goes to smallest bin etc.)
- The analytic Row_Number function computes the updated bin ranks, and the bin values are updated by simple addition
Recursive Subquery Factor for GBR with Temporary Table
Create Table and Index
DROP TABLE items_desc_temp / CREATE GLOBAL TEMPORARY TABLE items_desc_temp ( item_name VARCHAR2(30) NOT NULL, item_value NUMBER(8) NOT NULL, rn NUMBER ) ON COMMIT DELETE ROWS / CREATE INDEX items_desc_temp_N1 ON items_desc_temp (rn) /
Insert into Temporary Table
INSERT INTO items_desc_temp SELECT item_name, item_value, Row_Number () OVER (ORDER BY item_value DESC) rn FROM items;
RSF Query with Temporary Table
WITH bins AS (
SELECT LEVEL bin, :N_BINS n_bins FROM DUAL CONNECT BY LEVEL <= :N_BINS
), rsf (bin, item_name, item_value, bin_value, lev, bin_rank, n_bins) AS (
SELECT b.bin,
i.item_name,
i.item_value,
i.item_value,
1,
b.n_bins - i.rn + 1,
b.n_bins
FROM bins b
JOIN items_desc_temp i
ON i.rn = b.bin
UNION ALL
SELECT r.bin,
i.item_name,
i.item_value,
r.bin_value + i.item_value,
r.lev + 1,
Row_Number () OVER (ORDER BY r.bin_value + i.item_value),
r.n_bins
FROM rsf r
JOIN items_desc_temp i
ON i.rn = r.bin_rank + r.lev * r.n_bins
)
SELECT item_name, bin, item_value, bin_value
FROM rsf
ORDER BY item_value DESC
The idea here is that in the initial RSF query a subquery factor of items was joined on a calculated field, so the whole record set had to be read, and performance could be improved by putting that initial record set into an indexed temporary table ahead of the main query. We'll see in the performance testing section that this changes quadratic variation with problem size into linear variation.
Plain Old SQL Solution for TPA
WITH items_desc AS (
SELECT item_name, item_value,
Mod (Row_Number () OVER (ORDER BY item_value DESC), :N_BINS) + 1 bin
FROM items
)
SELECT item_name, bin, item_value, Sum (item_value) OVER (PARTITION BY bin) bin_total
FROM items_desc
ORDER BY item_value DESC
The idea here is that the TPA algorithm can be implemented in simple SQL using analyic functions.
- The subquery factor assigns the bins by taking the item rank in descending order of value and applying the modulo (N) function
- The main query returns the bin totals in addition by analytic summing by bin
Pipelined Function for GDY
Package
CREATE OR REPLACE PACKAGE Bin_Fit AS
TYPE bin_fit_rec_type IS RECORD (item_name VARCHAR2(100), item_value NUMBER, bin NUMBER);
TYPE bin_fit_list_type IS VARRAY(1000) OF bin_fit_rec_type;
TYPE bin_fit_cur_rec_type IS RECORD (item_name VARCHAR2(100), item_value NUMBER);
TYPE bin_fit_cur_type IS REF CURSOR RETURN bin_fit_cur_rec_type;
FUNCTION Items_Binned (p_items_cur bin_fit_cur_type, p_n_bins PLS_INTEGER) RETURN bin_fit_list_type PIPELINED;
END Bin_Fit;
/
CREATE OR REPLACE PACKAGE BODY Bin_Fit AS
c_big_value CONSTANT NUMBER := 100000000;
TYPE bin_fit_cur_list_type IS VARRAY(100) OF bin_fit_cur_rec_type;
FUNCTION Items_Binned (p_items_cur bin_fit_cur_type, p_n_bins PLS_INTEGER) RETURN bin_fit_list_type PIPELINED IS
l_min_bin PLS_INTEGER := 1;
l_min_bin_val NUMBER;
l_bins SYS.ODCINumberList := SYS.ODCINumberList();
l_bin_fit_cur_rec bin_fit_cur_rec_type;
l_bin_fit_rec bin_fit_rec_type;
l_bin_fit_cur_list bin_fit_cur_list_type;
BEGIN
l_bins.Extend (p_n_bins);
FOR i IN 1..p_n_bins LOOP
l_bins(i) := 0;
END LOOP;
LOOP
FETCH p_items_cur BULK COLLECT INTO l_bin_fit_cur_list LIMIT 100;
EXIT WHEN l_bin_fit_cur_list.COUNT = 0;
FOR j IN 1..l_bin_fit_cur_list.COUNT LOOP
l_bin_fit_rec.item_name := l_bin_fit_cur_list(j).item_name;
l_bin_fit_rec.item_value := l_bin_fit_cur_list(j).item_value;
l_bin_fit_rec.bin := l_min_bin;
PIPE ROW (l_bin_fit_rec);
l_bins(l_min_bin) := l_bins(l_min_bin) + l_bin_fit_cur_list(j).item_value;
l_min_bin_val := c_big_value;
FOR i IN 1..p_n_bins LOOP
IF l_bins(i) < l_min_bin_val THEN
l_min_bin := i;
l_min_bin_val := l_bins(i);
END IF;
END LOOP;
END LOOP;
END LOOP;
END Items_Binned;
SQL Query
SELECT item_name, bin, item_value, Sum (item_value) OVER (PARTITION BY bin) bin_value
FROM TABLE (Bin_Fit.Items_Binned (
CURSOR (SELECT item_name, item_value FROM items ORDER BY item_value DESC),
:N_BINS))
ORDER BY item_value DESC
The idea here is that procedural algorithms can often be implemented more efficiently in PL/SQL than in SQL.
- The first parameter to the function is a strongly-typed reference cursor
- The SQL call passes in a SELECT statement wrapped in the CURSOR keyword, so the function can be used for any set of records that returns name and numeric value pairs
- The item records are fetched in batches of 100 using the LIMIT clause to improves efficiency
Performance Testing
I tested performance of the various queries using my own benchmarking framework across grids of data points, with two data sets to split the queries into two sets based on performance.
I presented on this approach to benchmarking SQL at the Ireland Oracle User Group conference in March 2017, Dimensional Performance Benchmarking of SQL – IOUG Presentation.
Query Modifications for Performance Testing
- The RSF query with staging table was run within a pipelined function in order to easily include the insert in the timings
- A system context was used to pass the bind variables as the framework runs the queries from PL/SQL, not from SQL*Plus
- I found that calculating the bin values using analytic sums, as in the code above, affected performance, so I removed this for clarity of results, outputting only item name, value and bin
Test Data Sets
For a given depth parameter, d, random numbers were inserted within the range 0-d for d-1 records. The insert was:
INSERT INTO items SELECT 'item-' || n, DBMS_Random.Value (0, p_point_deep) FROM (SELECT LEVEL n FROM DUAL CONNECT BY LEVEL < p_point_deep);
The number of bins was passed as a width parameter, but note that the original, linked Model solution, MODO, hard-codes the number of bins to 3.
Test Results
Data Set 1 - Small
This was used for the following queries:
- MODO - Original Model for GDY
- MODB - Brendan's Generic Model for GDY
- RSFQ - Recursive Subquery Factor for GBR
Depth W3 W3 W3 Run Type=MODO D1000 1.03 1.77 1.05 D2000 3.98 6.46 5.38 D4000 15.79 20.7 25.58 D8000 63.18 88.75 92.27 D16000 364.2 347.74 351.99 Run Type=MODB Depth W3 W6 W12 D1000 .27 .42 .27 D2000 1 1.58 1.59 D4000 3.86 3.8 6.19 D8000 23.26 24.57 17.19 D16000 82.29 92.04 96.02 Run Type=RSFQ D1000 3.24 3.17 1.53 D2000 8.58 9.68 8.02 D4000 25.65 24.07 23.17 D8000 111.3 108.25 98.33 D16000 471.17 407.65 399.99
- Quadratic variation of CPU time with number of items
- Little variation of CPU time with number of bins, although RSFQ seems to show some decline
- RSFQ is slightly slower than MODO, while my version of Model, MODB is about 4 times faster than MODO
Data Set 2 - Large
This was used for the following queries:
- RSFT - Recursive Subquery Factor for GBR with Temporary Table
- POSS - Plain Old SQL Solution for TPA
- PLFN - Pipelined Function for GDY
This table gives the CPU times in seconds across the data set:
Depth W100 W1000 W10000 Run Type=PLFN D20000 .31 1.92 19.25 D40000 .65 3.87 55.78 D80000 1.28 7.72 92.83 D160000 2.67 16.59 214.96 D320000 5.29 38.68 418.7 D640000 11.61 84.57 823.9 Run Type=POSS D20000 .09 .13 .13 D40000 .18 .21 .18 D80000 .27 .36 .6 D160000 .74 1.07 .83 D320000 1.36 1.58 1.58 D640000 3.13 3.97 4.04 Run Type=RSFT D20000 .78 .78 .84 D40000 1.41 1.54 1.7 D80000 3.02 3.39 4.88 D160000 6.11 9.56 8.42 D320000 13.05 18.93 20.84 D640000 41.62 40.98 41.09
- Linear variation of CPU time with number of items
- Little variation of CPU time with number of bins for POSS and RSFT, but roughly linear variation for PLFN
- These linear methods are much faster than the earlier quadratic ones for larger numbers of items
- Its approximate proportionality of time to number of bins means that, while PLFN is faster than RSFT for small number of bins, it becomes slower from around 50 bins for our problem
- The proportionality to number of bins for PLFN presumably arises from the step to find the bin of minimum value
- The lack of proportionality to number of bins for RSFT may appear surprising since it performs a sort of the bins iteratively: However, while the work for this sort is likely to be proportional to the number of bins, the number of iterations is inversely proportional and thus cancels out the variation
Solution Quality
The methods reported above implement three underlying algorithms, none of which guarantees an optimal solution. In order to get an idea of how the quality compares, I created new versions of the second set of queries using analytic functions to output the difference between minimum and maximum bin values, with percentage of the maximum also output. I ran these on the same grid, and report below the results for the four corners.
Method: PLFN RSFT POSS Point: W100/D20000 Diff/%: 72/.004% 72/.004% 19,825/1% Point: W100/D640000 Diff/%: 60/.000003% 60/.000003% 633499/.03% Point: W10000/D20000 Diff/%: 189/.9% 180/.9% 19,995/67% Point: W10000/D640000 Diff/%: 695/.003% 695/.003% 639,933/3%
The results indicate that GDY (Greedy Algorithm) and GBR (Greedy Algorithm with Batched Rebalancing) generally give very similar quality results, while TPA (Team Picking Algorithm) tends to be quite a lot worse.
Extended Problem: Finding the Number of Bins Required
An important extension to the problem is when the bins have fixed capacity, and it is desired to find the minimum number of bins, then spread the items evenly between them. As mentioned at the start, I posted extensions to two of my solutions on an OTN thread, and I reproduce them here. It turns out to be quite easy to make the extension. The remainder of this section is just lifted from my OTN post and refers to the table of the original poster.
Start OTN Extract
So how do we determine the number of bins? The total quantity divided by bin capacity, rounded up, gives a lower bound on the number of bins needed. The actual number required may be larger, but mostly it will be within a very small range from the lower bound, I believe (I suspect it will nearly always be the lower bound). A good practical solution, therefore, would be to compute the solutions for a base number, plus one or more increments, and this can be done with negligible extra work (although Model might be an exception, I haven't tried it). Then the bin totals can be computed, and the first solution that meets the constraints can be used. I took two bin sets here.
SQL POS
WITH items AS (
SELECT sl_pm_code item_name, sl_wt item_amt, sl_qty item_qty,
Ceil (Sum(sl_qty) OVER () / :MAX_QTY) n_bins
FROM ow_ship_det
), items_desc AS (
SELECT item_name, item_amt, item_qty, n_bins,
Mod (Row_Number () OVER (ORDER BY item_qty DESC), n_bins) bin_1,
Mod (Row_Number () OVER (ORDER BY item_qty DESC), n_bins + 1) bin_2
FROM items
)
SELECT item_name, item_amt, item_qty,
CASE bin_1 WHEN 0 THEN n_bins ELSE bin_1 END bin_1,
CASE bin_2 WHEN 0 THEN n_bins + 1 ELSE bin_2 END bin_2,
Sum (item_amt) OVER (PARTITION BY bin_1) bin_1_amt,
Sum (item_qty) OVER (PARTITION BY bin_1) bin_1_qty,
Sum (item_amt) OVER (PARTITION BY bin_2) bin_2_amt,
Sum (item_qty) OVER (PARTITION BY bin_2) bin_2_qty
FROM items_desc
ORDER BY item_qty DESC, bin_1, bin_2
SQL Pipelined
SELECT osd.sl_pm_code item_name, osd.sl_wt item_amt, osd.sl_qty item_qty,
tab.bin_1, tab.bin_2,
Sum (osd.sl_wt) OVER (PARTITION BY tab.bin_1) bin_1_amt,
Sum (osd.sl_qty) OVER (PARTITION BY tab.bin_1) bin_1_qty,
Sum (osd.sl_wt) OVER (PARTITION BY tab.bin_2) bin_2_amt,
Sum (osd.sl_qty) OVER (PARTITION BY tab.bin_2) bin_2_qty
FROM ow_ship_det osd
JOIN TABLE (Bin_Even.Items_Binned (
CURSOR (SELECT sl_pm_code item_name, sl_qty item_value,
Sum(sl_qty) OVER () item_total
FROM ow_ship_det
ORDER BY sl_qty DESC, sl_wt DESC),
:MAX_QTY)) tab
ON tab.item_name = osd.sl_pm_code
ORDER BY osd.sl_qty DESC, tab.bin_1
Pipelined Function
CREATE OR REPLACE PACKAGE Bin_Even AS
TYPE bin_even_rec_type IS RECORD (item_name VARCHAR2(100), item_value NUMBER, bin_1 NUMBER, bin_2 NUMBER);
TYPE bin_even_list_type IS VARRAY(1000) OF bin_even_rec_type;
TYPE bin_even_cur_rec_type IS RECORD (item_name VARCHAR2(100), item_value NUMBER, item_total NUMBER);
TYPE bin_even_cur_type IS REF CURSOR RETURN bin_even_cur_rec_type;
FUNCTION Items_Binned (p_items_cur bin_even_cur_type, p_bin_max NUMBER) RETURN bin_even_list_type PIPELINED;
END Bin_Even;
/
SHO ERR
CREATE OR REPLACE PACKAGE BODY Bin_Even AS
c_big_value CONSTANT NUMBER := 100000000;
c_n_bin_sets CONSTANT NUMBER := 2;
TYPE bin_even_cur_list_type IS VARRAY(100) OF bin_even_cur_rec_type;
TYPE num_lol_list_type IS VARRAY(100) OF SYS.ODCINumberList;
FUNCTION Items_Binned (p_items_cur bin_even_cur_type, p_bin_max NUMBER) RETURN bin_even_list_type PIPELINED IS
l_min_bin SYS.ODCINumberList := SYS.ODCINumberList (1, 1);
l_min_bin_val SYS.ODCINumberList := SYS.ODCINumberList (c_big_value, c_big_value);
l_bins num_lol_list_type := num_lol_list_type (SYS.ODCINumberList(), SYS.ODCINumberList());
l_bin_even_cur_rec bin_even_cur_rec_type;
l_bin_even_rec bin_even_rec_type;
l_bin_even_cur_list bin_even_cur_list_type;
l_n_bins PLS_INTEGER;
l_n_bins_base PLS_INTEGER;
l_is_first_fetch BOOLEAN := TRUE;
BEGIN
LOOP
FETCH p_items_cur BULK COLLECT INTO l_bin_even_cur_list LIMIT 100;
EXIT WHEN l_Bin_Even_cur_list.COUNT = 0;
IF l_is_first_fetch THEN
l_n_bins_base := Ceil (l_Bin_Even_cur_list(1).item_total / p_bin_max) - 1;
l_is_first_fetch := FALSE;
l_n_bins := l_n_bins_base;
FOR i IN 1..c_n_bin_sets LOOP
l_n_bins := l_n_bins + 1;
l_bins(i).Extend (l_n_bins);
FOR k IN 1..l_n_bins LOOP
l_bins(i)(k) := 0;
END LOOP;
END LOOP;
END IF;
FOR j IN 1..l_Bin_Even_cur_list.COUNT LOOP
l_bin_even_rec.item_name := l_bin_even_cur_list(j).item_name;
l_bin_even_rec.item_value := l_bin_even_cur_list(j).item_value;
l_bin_even_rec.bin_1 := l_min_bin(1);
l_bin_even_rec.bin_2 := l_min_bin(2);
PIPE ROW (l_bin_even_rec);
l_n_bins := l_n_bins_base;
FOR i IN 1..c_n_bin_sets LOOP
l_n_bins := l_n_bins + 1;
l_bins(i)(l_min_bin(i)) := l_bins(i)(l_min_bin(i)) + l_Bin_Even_cur_list(j).item_value;
l_min_bin_val(i) := c_big_value;
FOR k IN 1..l_n_bins LOOP
IF l_bins(i)(k) < l_min_bin_val(i) THEN
l_min_bin(i) := k;
l_min_bin_val(i) := l_bins(i)(k);
END IF;
END LOOP;
END LOOP;
END LOOP;
END LOOP;
END Items_Binned;
END Bin_Even;
Output POS
Note BIN_1 means bin set 1, which turns out to have 4 bins, while bin set 2 then necessarily has 5.
ITEM_NAME ITEM_AMT ITEM_QTY BIN_1 BIN_2 BIN_1_AMT BIN_1_QTY BIN_2_AMT BIN_2_QTY --------------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- 1239606-1080 4024 266 1 1 25562 995 17482 827 1239606-1045 1880 192 2 2 19394 886 14568 732 1239606-1044 1567 160 3 3 18115 835 14097 688 1239606-1081 2118 140 4 4 18988 793 17130 657 1239606-2094 5741 96 1 5 25562 995 18782 605 ... 1239606-2107 80 3 4 2 18988 793 14568 732 1239606-2084 122 3 4 3 18988 793 14097 688 1239606-2110 210 2 2 3 19394 886 14097 688 1239606-4022 212 2 3 4 18115 835 17130 657 1239606-4021 212 2 4 5 18988 793 18782 605
Output Pipelined
ITEM_NAME ITEM_AMT ITEM_QTY BIN_1 BIN_2 BIN_1_AMT BIN_1_QTY BIN_2_AMT BIN_2_QTY --------------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- 1239606-1080 4024 266 1 1 20627 878 15805 703 1239606-1045 1880 192 2 2 18220 877 16176 703 1239606-1044 1567 160 3 3 20425 878 15651 701 1239606-1081 2118 140 4 4 22787 876 14797 701 1239606-2094 5741 96 4 5 22787 876 19630 701 ... 1239606-2089 80 3 4 1 22787 876 15805 703 1239606-2112 141 3 4 2 22787 876 16176 703 1239606-4022 212 2 1 1 20627 878 15805 703 1239606-4021 212 2 2 1 18220 877 15805 703 1239606-2110 210 2 3 2 20425 878 16176 703
End OTN Extract
Conclusions
- Various solutions for the balanced number partitioning problem have been presented, using Oracle's Model clause, Recursive Subquery Factoring, Pipelined Functions and simple SQL
- The performance characteristics of these solutions have been tested across a range of data sets
- As is often the case, the best solution depends on the shape and size of the data set
- A simple extension has been shown to allow determining the number of bins required in the bin-fitting interpretation of the problem
- Replacing a WITH clause with a staging table can be a useful technique to allow indexed scans
Get the code here: Brendan's repo for interesting SQL





Most interesting and enlightening stuff, Brendan, thanks for sharing all this!
Hi,
Thanks a lot for sharing “Brendan’s Generic Model for GDY” – it’s been really useful.
I’m doing the bin fitting in chunks of rows and not all at once so I altered it to my needs to get the current bin sizes from another table for the initialization.
Thanks again,
Mor
Hi, Thanks for offering so many solutions to choose from 🙂
I’m after something similar, I would be interested to use “Brendan’s Generic Model for GDY”, for varied number of bins. I tried this solution on my toad client, and :N_Bins bind variable is not visible (not sure if it’s my version ??) when I tried to run the query.
Say, if I have a table (test) which tells me how many bins (bin_count) to split on, how can I use this count value in the above algorithm.
with test_tab
as (select bin_count from test).
Many thanks in advance..